Khái Niệm Tam Giác Đều là gì? Tính chất và các ứng dụng của tam giác đều

Khái Niệm Tam Giác Đều là một định nghĩa nhiều bạn đang cần tìm hiểu thông tin, trong bài viết này chúng ta sẽ làm rõ về khái niệm tam giác đều đúng nhất theo các tài liệu chính xác.

Hình tam giác đều thường sẽ gắn liền với nhiều dạng bài tập khác nhau từ đơn giản tới nâng cao để thử thách người học nhờ nhiều tính chất cực thú vị của chúng. Cùng xem những kiến thức bên dưới để biết thêm về tam giác đều và giải các bài toán liên quan.

1. Định nghĩa hình tam giác là gì?

Hình tam giác là hình học có ba đỉnh là ba điểm không thẳng hàng và ba đoạn thẳng nối các đỉnh với nhau tạo thành ba cạnh. Tam giác luôn là một đa giác đơn và là đa giác lồi.

Trong thực tế có nhiều dạng tam giác khác nhau như: Tam giác cân, tam giác vuông, tam giác đều, tam giác bình thường.

Để hiểu rõ hơn về hình tam giác, mời bạn tham khảo bài viết Hình tam giác là gì?.

2. Khái Niệm Tam Giác Đều là gì?

Tam giác đều là mộ trường hợp đặc biệt của hình tam giác bởi chúng có ba cạnh bằng nhau. Hình tam giác đều còn được gọi là đa giác đều với số cạnh bằng ba.

Hệ quả:

• Trong tam giác đều, mỗi góc bằng 60°
• Nếu trong một tam giác có ba góc bằng nhau thì đó là tam giác đều.
• Nếu một tam giác cân có 1 góc bằng 60° thì đó là tam giác đều.

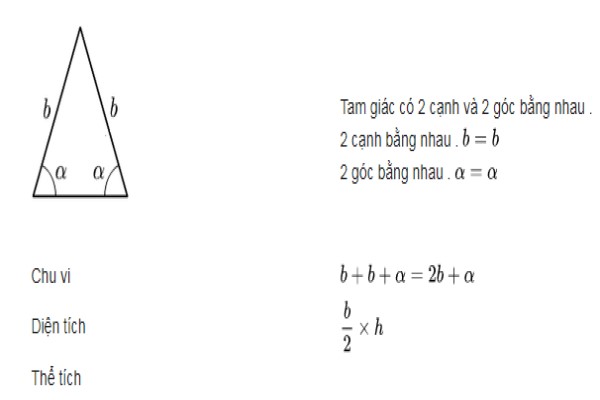
Tính chất hình tam giác đều

• Trong một tam giác đều, mỗi góc bằng 60°.
• Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.
• Nếu một tam giác cân có một góc bằng 60° thì tam giác đó là tam giác đều.
• Trong tam giác đều, đường trung tuyến của tam giác đồng thời là đường cao và đường phân giác của tam giác đó.

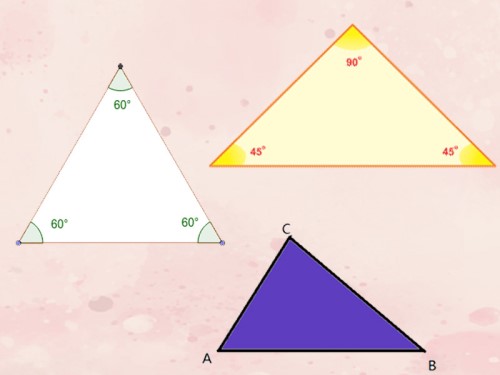
Dấu hiệu nhận biết tam giác đều

• Tam giác có 3 cạnh bằng nhau là tam giác đều.
• Tam giác có 3 góc bằng nhau là tam giác đều.
• Tam giác cân có một góc bằng 60° là tam giác đều.
• Tam giác có 2 góc bằng 60° là tam giác đều.

3. Công thức liên quan tam giác đều

Công thức tính chu vi tam giác đều

Công thức: P = 3.a

Trong đó:

• P: Chu vi tam giác đều.
• a: Chiều dài cạnh của tam giác.

Công thức tính chu vi tam giác đều

Công thức: S = a .(√3)/4

Trong đó:

• a: Độ dài các cạnh của tam giác đều.
• S: Diện tích của tam giác đều.

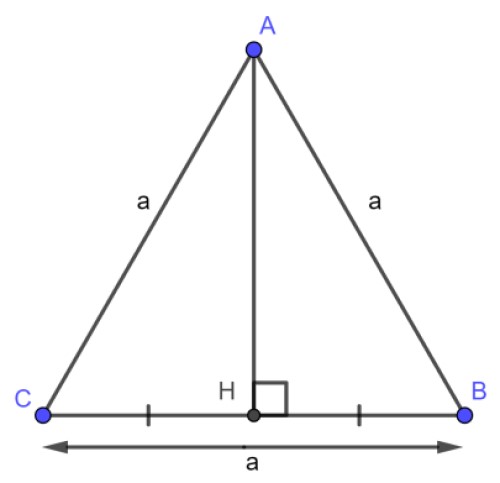
Công thức tính đường cao trong tam giác đều

Công thức tính đường cao trong tam giác đều: h = a.(√3)/2

Trong đó:

• a: Độ dài các cạnh của tam giác đều.
• h: Chiều cao của hình tam giác đều.

4. Bài tập liên quan tới tam giác đều

Bài tập 1: Cho tam giác ABC có ∠C = ∠B và ∠A = 60°. Chứng minh tam giác ABC đều?

Bài giải

Xét tam giác ABC có góc ∠C + ∠B + ∠A = 180°.

Mà theo gt ta có ∠C = ∠B.

Suy ra 2∠C + ∠A = 180°.

=> 2∠C = 180° – ∠A = 180° – 60° = 120°.

=> ∠C = 120° : 2 = 60°.

Ta có ∠C = ∠B = 60° và ∠A = 60° (gt).

=> Tam giác ABC có 3 góc bằng 60° là tam giác đều (đpcm).

Bài tập 2: Cho tam giác đều ABC có AB bằng 4 (cm). Hãy tính đường cao và diện tích của tam giác đều?

Bài giải:

Đường cao hình tam giác đều ABC là:

h = a.(√3)/2 = 8√3 (cm).

Diện tích hình tam giác đều ABC là:

S = a .(√3)/4 = 4 .(√3)/4 = 4√3 (cm ).

Bài tập 3: Cho tam giác ABC đều có BC = 6 (cm). Hỏi chu vi và diện tích tam giác đều bằng bao nhiêu?

Bài giải:

Chu vi của hình tam giác đều ABC là:

P = 3.a = 3.6 = 18 (cm).

Diện tích hình tam giác đều ABC là:

S = a .(√3)/4 = 6 .(√3)/4 = 9√3 (cm ).

5. Ứng dụng của tam giác đều trong đời sống

Trong đời sống, tam giác đều ứng dụng vào rất nhiều đồ vật có thể kể đến như:

• Đồ gia dụng: Kệ treo tường, bàn, ghế, khung ảnh trang trí, dĩa,…
• Dụng cụ học tập: Thước, mô hình mô tả hình tam giác đều,…

Trên đây là những tổng hợp của Reviews365 về Khái Niệm Tam Giác Đều là gì. Bạn cũng có thể để lại ý kiến của mình về vấn đề này tại phần bình luận dưới đây! Chúng ta hãy cùng đóng góp và chia sẻ kiến thức nhé! Chân thành cảm ơn bạn!

Reviews365 là website chia sẻ kiến thức miễn phí bằng tiếng Việt, tiếng Anh, giúp bạn tìm hiểu thông tin và giải trí sau giờ học tập và làm việc căng thẳng. Chúng tôi mong muốn mang lại nhiều điều thú vị, giao lưu với BQT Reviews365 tại fanpage